Shufflin'
Abstract
Folks often point to the TCO shuffler, and mulligan outcomes in particular, as not mirroring real life experience. Here we review TCO's methods for shuffling and handling mulligans. We also simulate a large number of mulligans and observe the results.
Is TCO bad at shuffling?!
Method
Our methods for this analysis are simple - we will present and review the TCO code responsible shuffling and handling mulligans.
We also simulated one million mulligans using the same methods and libraries that TCO itself uses. Those results are presented below.
Results
The snippet of code below isolates our entry point into TCO's mulligan handling.
We see a method named takeMulligan attached a player class.
Lines, 6-8 move each card from our hand back to the deck. Then the deck is shuffled on line 9. We then draw cards, one fewer than we had initially, and finally on line 11 we set a flag indicating that a mulligan has been taken.
Things are looking fairly innocent so far. The steps match the actions a player
would take in a live game pretty closely. It's worth noting that the keyword this
in our TCO snippets will refer to one of the players in our game.
Ok, let's drill into shuffleDeck.
Well now, we have a bit more going on with a simple shuffle.
Lines 5-8 send out a message to the rest of the system indicating that the player in question has shuffled their deck. That's handy and interesting, but not directly related to our present journey.
Line 9 replaces the player's current deck with whatever _.shuffle spits out.
We'll circle back to this.
Lines 10-19 are special handling for the card Near-Future Lens. Post shuffle, it is meant to ensure that the top card of your deck is turned face up, and each other turned face down. We then add a message to the game chat declaring the identity of the face-up card.
Again, TCO's method is fairly straightforward, ignoring some fancy footwork to handle a certain special future lens.
In fact, all the heavy lifting is happening in that _.shuffle(this.deck) on
line 9 that we breezed by. So what's going on there?
The underscore ( _ ) references a third party library called... well...
underscore. Much like how you might reference a prior work for a research paper,
TCO is sitting on the shoulders of giants and borrowing a shuffle implementation
from somewhere else. Underscore is a popular, if somewhat old and out of
fashion, utility library. Today's hipster programmers might scoff at underscore for
being last year's model, but (as we will see) its methods are generally sound.
We'll continue on, but first it's worth noting that Underscore itself gets around 12 million weekly downloads. Its spiritual successor, lodash (see what they did there?), is downloaded ~50 million times weekly. These are battle-hardened utility libraries, all but ubiquitous in the world of web applications forged in the mid-late 2010s.
We shift gears from the TCO code repository and jump into Underscore.
Underscore's shuffle is not terribly exciting. Our intuition from reading this
one-liner says that "shuffling" is being treated like sampling as much as possible.
I.e. keep taking a random thing from your bag of things until there are no
things left.
Le's crack open sample and see if the code matches our intuition.
The first half of this method is boilerplate and safeguards, making sure
everything it was given to work with is in reasonable shape. And if that pesky
Infinity we encountered made you suspicious, line 8 here ensures we never
actually try to do more sampling than we have things to sample from.
The business end of sample resides in lines 10 through 15.
Essentially what's happening is this, our array (list) has two sections:
- In the first section, we keep a running tally of the items that have been selected thus far in the sampling.
- In the second section, we hold the remaining items not yet selected.
Each time we go to take another sample, a random (we'll get back to that) item is chosen from the second section and placed at the end of the first section. In this way, the first section grows and the second section shrinks. If we stick to this process until we run out of items in the second section, what's in the first will be a completely shuffled version of our original ~~deck~~ list.
What we've just described is known as the Fisher–Yates shuffle and is among the most popular shuffle algorithms used in the wild today.
The final piece of code we may want to look at is the guts of our random number generator - it does reside at the heart of our algorithm after all.
JavaScript, the language TCO is written in, itself has a native random number generator. While JavaScript may have some less-than-good parts, as of 2024 it still holds reasonable claim to being the most popular programming language in the world.
Our method here is a thin wrapper around JavaScript's own
native method that lets us pick an integer between 1 and 36 instead of
floating-point number in the range [0-1).
...
We find TCO's code for shuffling to be sound. Let's run some mulligan simulations.
A common remark from Crucible goers is that they very often get back essentially the same hand (minus one card) after a mulligan. Our lab simulated one million mulligans using TCO's methodology, the tables below show how often we observed cards from our original starting hand appearing in the post mulligan hand.
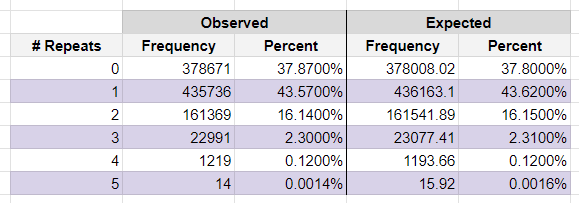
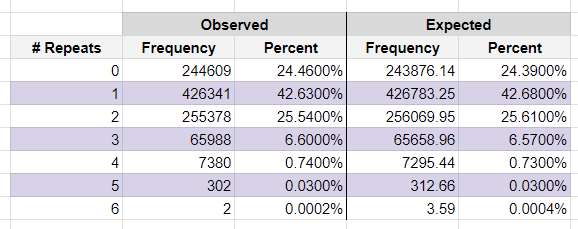
Above we show the complete results of our trials using a starting hand of 6 - how often the post-mulligan hand contained a certain number of repeat cards from our original hand. Below we show the same but for a starting hand of 7. We also include expected frequencies for comparison.
We find our observations match the expected frequencies very closely.
If TCO isn't bad shuffling, why do folks report a different experience? We offer a couple potential explanations to consider.
First, while we found TCO's method to be a good approximation of ideal shuffling the same is not necessarily true of the way humans mix cards. When performing a mulligan, it is not uncommon for a human to intentionally spread the cards from their starting hand throughout their deck - either directly or via a pile shuffle. With this as a starting point, it's very unlikely that a handful of pile and riffle shuffles will put more than two or three of the cards from our starting hand within the same six card range. In this light, it may be fair to say that the TCO experience doesn't mirror real life shuffling simply because TCO is closer to truly random.
Second, repeats will legitimately show up often. The first player should see at least two repeat cards about a third of the time after a mulligan. The second player should see at least two repeat cards about 20% of the time. That's not accounting for duplicates in a deck or the way that TCO sorts cards in hand, adding to a "fixed point" illusion. A player expecting a bad shuffle may see exactly that.
In summary, we believe the TCO method of shuffling to be about as good as can be hoped for. It's possible that this does not mirror human shuffling patterns exactly, but doing so would mean intentionally introducing elements to make our shuffles less random.
Think the lab missed something? We invite folks to review the code, run some simulations, or keep a record of each hand and mulligan as they play.